Basis vectors
Contents
5. Find another basis for R^5
%lets just take a set of vectors V = randi([0,10],5) %If the rank is 5, this is a basis rank(V)
V =
8 6 5 4 10
0 2 2 4 8
10 5 5 10 1
8 10 6 0 2
5 6 7 9 3
ans =
5
Now find the vector w in the new basis
w = [1;2;3;4;5] c = V\w
w =
1
2
3
4
5
c =
-0.4686
0.9841
-0.3015
0.4415
-0.1414
Check
V*c
ans =
1.0000
2.0000
3.0000
4.0000
5.0000
6. Orthonormal basis
1. Find a non-standard orthonormal basis for R^2 and R^3 Use the Gram-Schmidt Process
%first, a random set of vectors V = randi([0,10],2) %Take the first one and normalize v1 = V(:,1); e1 = v1 / sqrt(v1'*v1) %The norm is now 1 e1'*e1
V =
7 7
1 1
e1 =
0.9899
0.1414
ans =
1.0000
%Take the second vector and make it orthogonal v2 = V(:,2); c = v2'*e1; v = v2 - c*e1 %check v'*e1
v =
1.0e-15 *
0.8882
0.1110
ans =
8.9495e-16
And normalize
e2 = v / sqrt(v'*v)
%The norm is now 1
e2'*e2
e2 =
0.9923
0.1240
ans =
1.0000
The basis is then
[e1,e2]
ans =
0.9899 0.9923
0.1414 0.1240
The same for R^3
%first, a random set of vectors V = randi([0,10],3) for i = 1:3 %cycle trough the vectors v = V(:,i); for j = 1:(i-1) %go through all the previous vectors c = v'*e(:,j); v = v - c*e(:,j); end e(:,i) = v / sqrt(v'*v); % normalize end e
V =
7 7 3
5 9 7
8 9 2
e =
0.5959 -0.4222 0.6832
0.4256 0.8874 0.1771
0.6810 -0.1852 -0.7085
%For and R^n, as a function %function [ e ] = GramSchmidt( V, N ) %%GRAMSCHMIDT % for i = 1:N %cycle trough the vectors % v = V(:,i); % for j = 1:(i-1) %go through all the previous vectors % c = v'*e(:,j); % v = v - c*e(:,j); % end % e(:,i) = v / sqrt(v'*v); % normalize % end %end N=4 ; V = randi([0,10],N) ; GramSchmidt(V,N)
ans =
0 0.8943 0.4410 0.0764
0.7493 -0.2615 0.5680 -0.2182
0.4683 0.0601 -0.2674 0.8400
0.4683 0.3582 -0.6414 -0.4909
7.
n = 100;
dx = 2*pi/n;
x = linspace(-pi,pi,n+1); x(n+1)=[];
% Functions cos(x) and sin(2x)
f1 = cos(x);
f2 = sin(2*x);
norm1 = sqrt( f1*f1'*dx )
norm2 = sqrt( f2*f2'*dx )
product = f1*f2'*dx
norm1 =
1.7725
norm2 =
1.7725
product =
-2.5810e-16
How about sin(nx) and cos(nx)
n1=1; n2=2; n3=3; n4=4;
f1 = cos(n1*x);
f2 = sin(n2*x);
f3 = cos(n3*x);
f4 = sin(n4*x);
norm1 = sqrt( f1*f1'*dx )
norm2 = sqrt( f2*f2'*dx )
%always 1.7725
norm1 =
1.7725
norm2 =
1.7725
product1 = f1*f2'*dx product2 = f1*f3'*dx product3 = f2*f4'*dx
product1 = -2.5810e-16 product2 = -3.9064e-16 product3 = 4.5342e-17
Functions cos(nx) and sin(nx) form a basis find the vector x^2 in this basis
%find coefficients for a given n: N = 100; dx = 2*pi/N; x = linspace(-pi,pi,N+1); x(N+1)=[]; % Functions cos(nx) and sin(nx) n=2; b1 = cos(n*x); b2 = sin(n*x); %The function we are representing, x^2 f = x.*x; %Coefficients cn = (f1,b1)/(b1,b1) c1 = (f*b1'*dx) / ( b1*b1'*dx ); c2 = (f*b2'*dx) / ( b2*b2'*dx );
Find coefficients in the space of cos(nx) and sin(nx) for n<N-1
%function [ c1,c2 ] = Coefs( n ) %PRODUCT Summary of this function goes here % Detailed explanation goes here % for k = 1:n % N = 100; dx = 2*pi/N; % x = linspace(-pi,pi,N+1); x(N+1)=[]; % % % Functions cos(nx) and sin(nx) % b1 = cos((k-1)*x); b2 = sin((k-1)*x); % %The function we are representing, x^2 % f = x.*x; % % %Coefficients cn = (f1,b1)/(b1,b1) % c1(k) = (f*b1'*dx) / ( b1*b1'*dx ) ; % if k>1 % c2(k) = (f*b2'*dx) / ( b2*b2'*dx ); % else % c2(1) = 0; %sin(0x) = 0 % end % end %end N=10; [c1,c2] = Coefs(N)
c1 =
Columns 1 through 7
3.2905 -4.0013 1.0013 -0.4458 0.2513 -0.1613 0.1124
Columns 8 through 10
-0.0830 0.0638 -0.0507
c2 =
1.0e-14 *
Columns 1 through 7
0 0.0107 0.0213 -0.0977 0.0711 -0.0817 0.1812
Columns 8 through 10
-0.1315 0.0284 -0.0462
Now lets check if we get the original vector
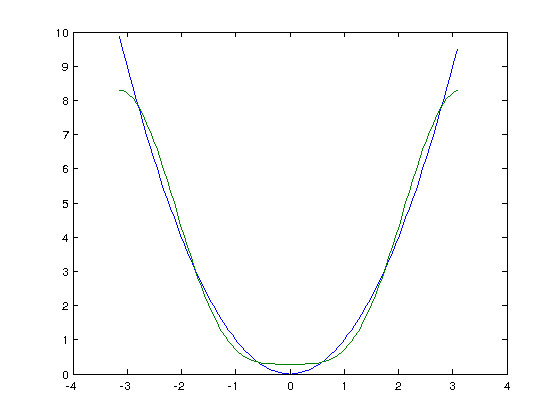
With N=3, we get an inaccurate result
k = 100; N = 3; dx = 2*pi/k; x = linspace(-pi,pi,k+1); x(k+1)=[]; f=0*x; for n = 1:N f = f + c1(n)*cos((n-1)*x); f = f + c2(n)*sin((n-1)*x); end plot(x,x.*x,x,f)
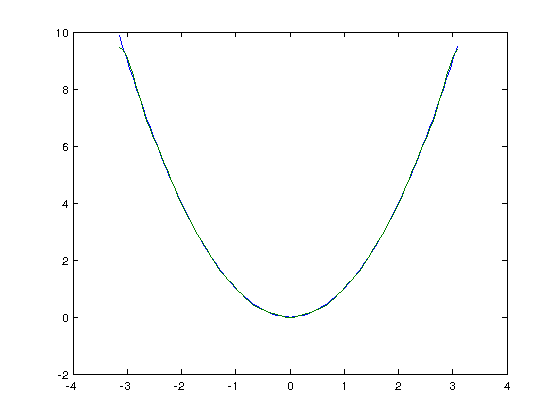
With N=10 it's much more accurate
k = 100; N = 10; dx = 2*pi/k; x = linspace(-pi,pi,k+1); x(k+1)=[]; f=0*x; for n = 1:N f = f + c1(n)*cos((n-1)*x); f = f + c2(n)*sin((n-1)*x); end plot(x,x.*x,x,f)